Imagina que das un paso hacia delante, luego giras 90º y das otro paso. Por último vuelves a girar 90º y das un tercer paso. ¿A qué distancia te encontrarás del punto de partida? Posiblemente, si lo pasos los has dado dentro de tu habitación, o incluso en la puerta de tu casa, la distancia a la que te encuentras del sitio donde estabas cuando comenzaste a andar sea ¡un paso! No es difícil imaginar el recorrido en forma de U con los tres pasos que has dado.
La geometría no euclídea fue descubierta y desarrollada independientemente por dos matemáticos en el siglo XIX: Nicolái Lobachevski y János Bolyai
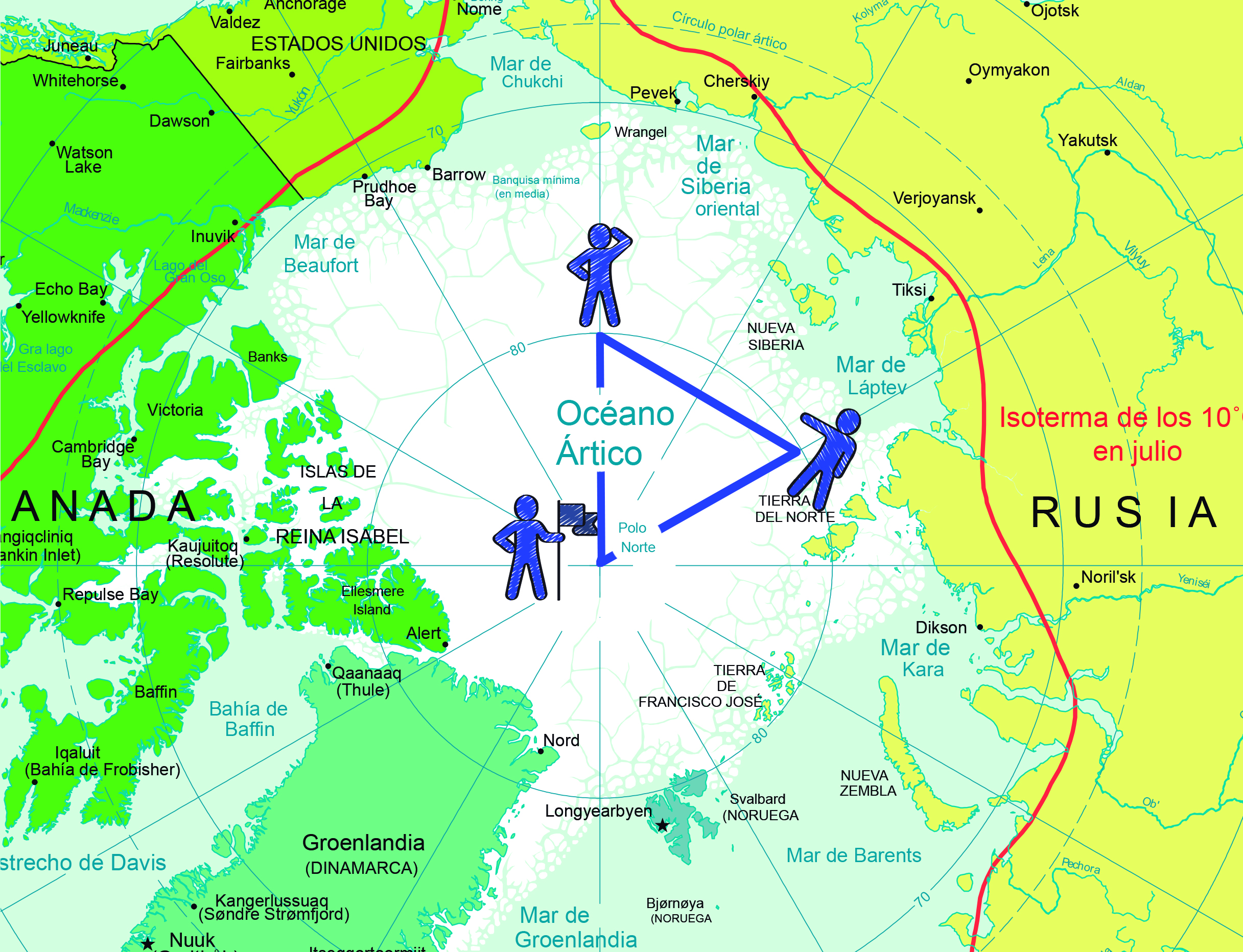
Ahora vamos a imaginar el ejercicio —recuerda: tres pasos con un ángulo de 90º— pero intentando volver al punto de partida. Parece imposible ¿verdad? Pues aunque no lo creas se puede hacer, aunque para ello tenemos que estar en un sitio muy concreto de la Tierra. ¿Sabes dónde? En uno de los polos. Piénsalo un momento: con el primer paso, bajamos, el segundo paso lo damos en un círculo concéntrico al polo y con el tercero subimos y ¡llegamos al primer punto! En el mapa de la derecha puedes ver como se realiza el itinerario —aunque con «pasos» enormes—.
Elon Musk puso de moda una versión de este problema en forma de acertijo: «One mile south, one mile east, one mile north»
Se llama geometría no euclídea a la geometría que no cumple todos los postulados de Euclides, especialmente el de que dos líneas paralelas nunca se cruzan. La geometría esférica de la Tierra es un ejemplo de geometría no euclídea ya que en la superficie esférica, las «líneas rectas» se convierten en arcos de grandes círculos que se cortan entre sí —en los polos—, y la suma de los ángulos en un triángulo puede ser mayor a 180 grados, lo cual contradice la geometría plana euclidiana.