Para jugar al Hackenbush, igual que para jugar al Nim, no necesitas fichas ni tablero. Pero sí papel, lápiz o colores, y goma de borrar. O te puedes descargar una versión para ordenador aquí.
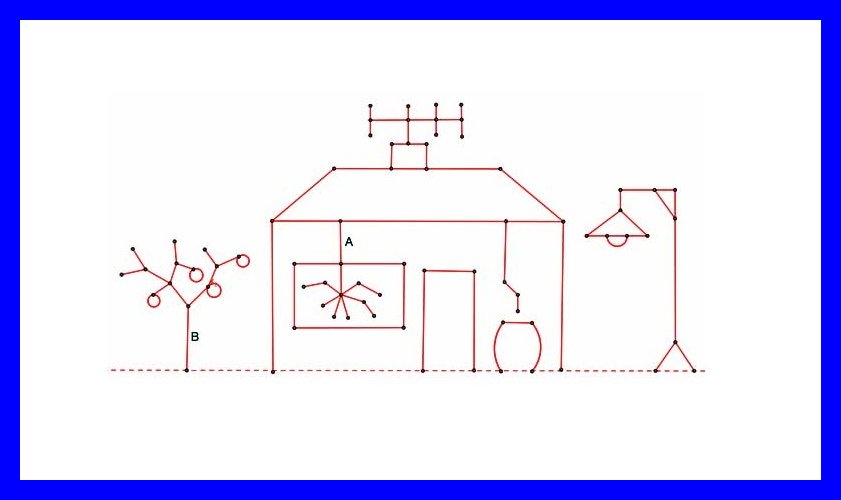
El juego no es tan sencillo como el Nim, pero se basa en los mismos principios. Para empezar, como en el Nim, imaginemos un grupo de líneas sin conectar. Ahora, pensemos también en puntos. A las líneas y los puntos, les llamaremos grafos. Un lado es cualquier línea que conecta dos puntos —también llamados nodos—, o un punto consigo mismo llamándose, en este caso, bucle. Como veréis, entre dos puntos determinados pueden coexistir dos lados o más. Todos los grafos se apoyan en una línea de base —la línea discontinua de la imagen— que no forma parte del grafo. Los nodos situados en ella se llaman nodos básicos.
El Hackenbush, inventado por John Conway, se basa en el Nim
Ahora podéis dibujar la imagen en un folio, o inventar otra imagen parecida —o muy distinta— con grafos y sobre una línea discontinua. ¡Comencemos la partida! Una jugada consiste en retirar un lado de manera que, al eliminarlo, quedan suprimidos también otros lados que dejan de estar conectados a la línea de base. Por ejemplo, al retirar el lado A, como en la imagen, quedarían eliminados todos los lados que forman la «araña» y la «ventana», y al retirar el lado B se elimina totalmente el «árbol».
Existen variantes (Blue-Red y Blue-Red-Green) en las que cada jugador debe retirar los lados de su color asignado
El juego no es tan sencillo como el Nim, pero se basa en los mismos principios: hay que asignar un número a cada grafo y estudiar la suma nim del total. El juego termina cuando uno de los jugadores ya no tiene ninguna línea que quitar, y pierde la partida.
Referencia: Martin Gardner. Ruedas, Vida y otras diversiones matemáticas
